Problem 11 – Largest product in a grid

In the Project Euler problem we have to calculate the maximum product of 4 adjacent numbers in a matrix 20×20. By adjacent we mean continuous numbers (side by side) in various directions, e.g. diagonal, horizontal or vertical. You can find the link to this problem here.

Table of Contents

• Introduction / Defining the problem
• Solving the problem
• Adjacency strategies
• Examples and Results

 

Introduction / Defining the problem

To make this problem a bit more challenging, we will try to solve it with a Design Patterns approach changing some of its aspects as follows:

• The matrix dimensions should be a variable or calculated at runtime (e.g. from importing a file).
• The matrix should be provided in plain text with space separated values, so that it’s easy to import such a matrix from a text file.
• The number of adjacent numbers should also be a variable. 
• There should be many types of adjacent numbers, not only diagonal, vertical and horizontal, and they should be provided as injected services. This enables us to extend the application to support any type of adjacent numbers (e.g. cross). This aspect will be solved with the Strategy Pattern.
• The type of calculation will also be independently injected. Specifically, in the Project Euler problem the calculation is a product. To tackle this we will use the Strategy Pattern again.

As a clarification, horizontal, vertical and diagonal adjacent numbers are shown in the matrix bellow.

• • vertical -> red
  • horizontal -> yellow
  • diagonal 45 degrees -> purple
  • diagonal 135 degrees -> green

Solving the problem

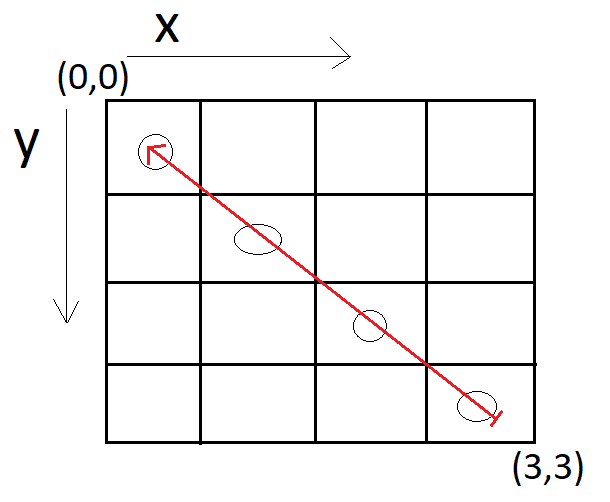
So, how we are going to solve this problem? First of all, we need the main algorithm that iterates through all rows and columns of the matrix shown below. As starting position we take the top left, so y represents the rows and x the columns of the matrix.

public List Solve(int[,] matrix)
{
   for (int y = 0; y < matrix.GetLength(0); y++)
   {
      for (int x = 0; x < matrix.GetLength(1); x++)
      {
         CalculateAdjusency(y, x, matrix);
      }
   }
   return this._parserStrategies;
}

We also assume that the matrix is a two dimensional array that stores integers.

Then, the CalculateAdjusency method will parse (if possible) the numbers from the specific point in the matrix, calculate their product (or whatever the operation may be) and update the maximum result.

private void CalculateAdjusency(int y, int x, int[,] matrix)
{
   foreach (var numberParserStrategy in this._parserStrategies)
   {
      if (!numberParserStrategy.IsInBounds(x, y, _adjusent, matrix))
         continue;
      var numbers = numberParserStrategy.GetNumbers(x, y, _adjusent, matrix);
      var result = _operation.Calculate(numbers);

      if (!numberParserStrategy.Max.HasValue || numberParserStrategy.Max < result)
         numberParserStrategy.UpdateMax(result, numbers);
   }
}

As we can see in the previous code, we iterate on every NumberParserStrategy and check if it can parse the adjacent numbers. If so, then we do the calculation. The operation and the adjacent variable are also instance variables.

Adjacency strategies

Looking further on the adjacent mode/strategies, we model them with the abstract NumberParserStrategy class which has two abstract methods.

public abstract class NumberParserStrategy
{
   // Giving the current position in the matrix it returns the related adjacent numbers.
   public abstract int[] GetNumbers(int x, int y, int adjacent, int[,] matrix);
   // It returns whether or not we can get the adjustment numbers.
   public abstract bool IsInBounds(int x, int y, int adjacent, int[,] matrix);
}

These functions are implemented by the following derived classes:

• Diagonal135DegreesNumberParser
• Diagonal45DegreesNumberParser
• HorizontalNumberParser
• VerticalNumberParser

With this design it’s easy to extend and add a new NumberParserStrategy.

Below we present the implementation of the Diagonal45DegreesNumberParser:

public class Diagonal45DegreesNumberParser : NumberParserStrategy
{
   public override bool IsInBounds(int x, int y, int adjacent, int[,] matrix)
   {
      int matrixX = matrix.GetLength(1);
      int x_diff = matrixX - x;
      int y_diff = y+1 - adjacent;

      if (x_diff >= adjacent && y_diff >= 0)
         return true;
      return false;
   }

   public override int[] GetNumbers(int x, int y, int adjacent, int[,] matrix)
   {
      int [] res = new int[adjacent];
      for (int a = 0; a < adjacent; a++)
      {
         res[a] = matrix[y, x];
         x++;
         y--;
      }
      return res;
   }

}

In a visual way the Diagonal45DegreesNumberParser in a 4×4 matrix can parse only 4 numbers (when the algorithm is on point (3,3) ):

 

Finally, we should end up with a ‘solver’ class that gets the NumberParserStrategies, Operation and adjacent as parameters.

public LargestProductInAGridSolver(int adjusent,
   List parserStrategies,
   IOperation operation)
{
   _adjusent = adjusent;
   _operation = operation;
   _parserStrategies = parserStrategies;
}

Examples and Results

Lastly, we present a couple of usage examples for the LargestProductInAGridSolver class:

With all the NumberParserStrategies, Product as the operation and 4 adjacent numbers (as the Project Euler problem) we can create the LargestProductInAGridSolver.

List parserStrategies = new List()
{
   new Diagonal45DegreesNumberParser(),
   new Diagonal135DegreesNumberParser(),
   new VerticalNumberParser(),
   new HorizontalNumberParser()
};

IOperation operation = new ProductOperation();
LargestProductInAGridSolver solver = new LargestProductInAGridSolver(4, parserStrategies, operation);
var res = solver.Solve(matrix);

And the result is:

Diagonal45DegreesNumberParser: Max:70600674 [87,97,94,89]
Diagonal135DegreesNumberParser: Max:40304286 [61,71,99,94]
VerticalNumberParser: Max:51267216 [66,91,88,97]
HorizontalNumberParser: Max:48477312 [78,78,96,83]
Maximum overall: Diagonal45DegreesNumberParser: Max:70600674 [87,97,94,89]

List parserStrategies = new List()
{
   new VerticalNumberParser(),
   new HorizontalNumberParser()
};

IOperation operation = new SumOperation();
LargestProductInAGridSolver solver = new LargestProductInAGridSolver(3, parserStrategies, operation);
var res = solver.Solve(matrix);

VerticalNumberParser: Max:276 [91,88,97]
HorizontalNumberParser: Max:257 [78,96,83]
Maximum overall: VerticalNumberParser: Max:276 [91,88,97]