Project Euler – Problem 17 – Number letter counts – A Design Patterns Approach

This article is part of the Design Patterns Approach series where we generalize and solve problems using Design Patterns.

First, we provide a solution for the problem 17 of the Project Euler. Then we redefine the problem to make it more generic in order to be able to solve a larger portion of similar problems using Design Patterns.

The solution of the original problem can be found on Github here and the code of the Design Patterns approach solution can be found here

The problem

If the numbers 1 to 5 are written out in words: one, two, three, four, five, then there are 3 + 3 + 5 + 4 + 4 = 19 letters used in total.

If all the numbers from 1 to 1000 (one thousand) inclusive were written out in words, how many letters would be used?

NOTE: Do not count spaces or hyphens. For example, 342 (three hundred and forty-two) contains 23 letters and 115 (one hundred and fifteen) contains 20 letters. The use of “and” when writing out numbers is in compliance with British usage.

Solution

The problem consist of two parts. The first part is to convert the numbers 1 to 1000 to words. The second part is the algorithm itself which iterates the numbers, converts them to words and then calculates the sum. We tackle both problems in the following sections.

Convert Numbers to word

The simplest case is the 1-digit number. We can use a lookup array for this purpose.

string[] one = new string[]
{
   "",
   "one",
   "two",
   "three",
   "four",
   "five",
   "six",
   "seven",
   "eight",
   "nine",
};

Zero is not needed. We add an empty string as the first element in order to be easier for the indexing when we access the elements. Then, we use the OneDigitNumberToWord method shown below to convert a single digit number to word

private string OneDigitNumberToWord(int number)
{
   return this.one[number];
}

The next case is the 2-digit numbers. For example:

56 => fiftysix

50 => fifty

40 => forty

45 => fortyfive

The second part of the number seems to be already covered by the one lookup array we created previously. For the tens we can have another lookup array as shown below:

string[] tenth = new string[]
{
   "",
   "",
   "twenty",
   "thirty",
   "forty",
   "fifty",
   "sixty",
   "seventy",
   "eighty",
   "ninety"
};

In this way, we can split the number to two digits and use the tenth and one arrays to resolve the digits to a single word. This approach seems to be working but there is an exception between numbers 10 to 19. Those numbers can be handled separately with another lookup array:

string[] ten = new string[]
{
   "ten",
   "eleven",
   "twelve",
   "thirteen",
   "fourteen",
   "fifteen",
   "sixteen",
   "seventeen",
   "eighteen",
   "nineteen"
};

Then, we create a method that first checks if the number is 1-digit. If its true then we call the OneDigitNumberToWord method to return the result. If not, we check if the number is between 10 and 19. In this case we return the proper element of the ten array. In any other case we split the digits and construct the word using the one and tenth lookup arrays we created previously.

private string TwoDigitNumberToWord(int number)
{
   int second = 0;
   if (number < 10)
   {
      return this.OneDigitNumberToWord(number);
   }
   else if (number >= 10 && number < 20)
   {
      second = Convert.ToInt32(number.ToString().Substring(1, 1));
      return this.ten[second];
   }

   int first = Convert.ToInt32(number.ToString().Substring(0, 1));
   second = Convert.ToInt32(number.ToString().Substring(1, 1));

   return this.tenth[first] + this.one[second];
}

Finally, we can handle the 3-digit numbers in a similar manner as we did with the 2-digit numbers. First, we split the number’s digits, then if the number has 3 digits, we delegate the 2 rightmost digits to TwoDigitNumberToWord method and construct the final word using the one array for the hundreds.

private string ThreeDigitNumberToWord(int number)
{
   int first = Convert.ToInt32(number.ToString().Substring(0, 1));
   string secondhalf = "";
   if (number.ToString().Length == 3)
   {
      secondhalf = this.TwoDigitNumberToWord(Convert.ToInt32(number.ToString().Substring(1, 2)));
      secondhalf = string.IsNullOrEmpty(secondhalf) == false ? "and " + secondhalf : string.Empty;
      return $"{this.one[first]} hundred {secondhalf}";
   }

   return this.TwoDigitNumberToWord(number);
}

The last step is to convert the 1000 number itself. We can handle this in the root method NumberToWord the main algorithm will use:

private string NumberToWord(int number)
{
   if(number.ToString().Length == 4)
   {
      return "one thousand";
   }
   return this.ThreeDigitNumberToWord(number);
}

The final solution

Now that we solved the number to word conversion we can move on to the main algorithm. This simply can be a loop though numbers from 1 to 1000 and for each iteration we convert the current number to a word and sum the word’s characters. The final code is shown below:

public void Solve()
{
   int from = 1;
   int to = 1000;

   int sum = 0;
   for(int i= from; i <= to; i++)
   {
      Console.WriteLine(this.NumberToWord(i));
      sum += this.NumberToWord(i).Replace(" ", string.Empty).Length;
   }
   Console.WriteLine("the sum is " + sum);
}

Note that we do not want to count spaces.

The final answer to the problem:

the sum is 21124

Redefine the problem

We can generalize and redefine the problem starting with the first sentence of the problem shown below

If the numbers 1 to 5 are written out in words: one, two, three, four, five, then there are 3 + 3 + 5 + 4 + 4 = 19 letters used in total.

From the above statement we extract three specific requirements.

1. We deal with numbers.
2. Translation from number to word ( f(1) = “one”).
3. Sum operation of the characters of all the numbers.

What we would like to do next is to generalize those requirements. The objective is to have a common algorithm in all cases that can be feed with different services/inputs each time.

After the generalization we define the problem as follows:

Translate each item in a list into another form and apply to each one of them an operation.

Define the cases the new solution should cover

In order to have a more clear sense of the problem, we are going to define a few cases the new solution should cover:

1. Original Problem from Project Euler
2. Calculate the average of the first 100 numbers
3. Calculate the average Rating of the first 100 BGG Entries (from boardgamegeek)
4. Calculate the average Title length of the first 100 BGG Entries
5. Calculate the sum of all Title characters of each song of Tool

Those cases should be solved by the same algorithm. At first glance they may seem different but they all are covered by the generic definition of the problem. For each of them, the only difference would be the different dependencies we will feed the algorithm.

In order to create a system with various degrees of freedom we should define the proper abstractions

Defining the abstractions

From the previous generic definition we can extract the following abstractions shown in the following table.

Requirement	Abstraction	Description
Items that will be translated	Subject	The Subject models each Item (e.g. numbers or other entries ) that the translation would be applied.
Translation of items	SubjectVisitor	This models the translation of a Subject to another form. For example, in case of a NumberSubject the translator will output the word of each Number ( f(1) = “one”).
in a list	SubjectIterator	We want some sort of iterator to provide the algorithm with Subjects. In case of NumberSubject the iterator provides the numbers 1 through 1000.
apply to them an operation	Operation	This models the operation that take place in each of the translated values of the Subjects. In case of the original problem the operation would be a SumOperation

Design Patterns that will be used

Below we display the Design Patterns that will be used to solve each of the problem.

Problem	Design Pattern	Purpose/Description
Translation of Items	Visitor	The SubjectVisitor will translate every Subject to the desired form.
Iteration of Items	Iterator	The SubjectIterator purpose is to enumerate through a range of Subjects.
Operation applied in each item	Strategy	The Operation class is responsible of applying an operation in each of the items
Iterators	Template	The abstract Iterator itself host a series of steps that one of them can be overridden from the subclasses. Will be explained further in Iterator section.

Crafting the algorithm

First, we iterate through all items and for each one of them we apply a translation and pass the result to an operation. At the end we get the final result of the Operation as shown in class Solver below:

public class Solver<T> : ISolver
   where T : Subject
{
   private readonly SubjectIterator<T> _iterator;
   private readonly SubjectVisitor _translator;
   private readonly Operation _operation;

   public Solver(SubjectIterator<T> iterator,
      SubjectVisitor translator,
      Operation operation)
   {
      _iterator = iterator;
      _translator = translator;
      _operation = operation;
   }

   public object Solve()
   {
      foreach (var s in _iterator.Next())
      {
         var translated = Translate(s);
         _operation.Push(translated);
      }

      var res = _operation.Pop();
      return res;
   }

   private object Translate(T s)
   {
      var translated = s.Accept(_translator);
      return translated;
   }
}

The Subject

The Subject models each item of the list. It could be a Number or any other entry. In order to cover all the cases mentioned earlier we have three different subclasses that inherit from the Subject abstract class.

public abstract class Subject
{
   public abstract object Accept(SubjectVisitor visitor);
}

public class Number : Subject
{
   public int Value { get; }

   public Number(int value)
   {
      Value = value;
   }

   public override object Accept(SubjectVisitor visitor)
   {
      return visitor.VisitNumber(this);
   }
}

public class BGGEntry : Subject
{
   public string Title { get; set; }
   public decimal Rating { get; set; }
   public int NumOfVotes { get; set; }

   public BGGEntry(string title, decimal rating, int numOfVotes)
   {
      Title = title;
      Rating = rating;
      NumOfVotes = numOfVotes;
   }

   public override object Accept(SubjectVisitor visitor)
   {
      return visitor.VisitBGGEntry(this);
   }
}

public class SongEntry : Subject
{
   public string Title { get; set; }
   public string Writers { get; set; }
   public int Year { get; set; }

   public SongEntry(string title, string writers, int year)
   {
      Title = title;
      Writers = writers;
      Year = year;
   }

   public override object Accept(SubjectVisitor visitor)
   {
      return visitor.VisitSongEntry(this);
   }
}

As we see from the above code one noticeable thing is the abstract Accept method that all subclasses needs to implement. This is part of the Visitor Pattern and will enable the visitor to visit each Subject.

The Iterator

The Iterator is responsible to feed the algorithm with Subject items. The type of Iterator all cases want is one that returns ordered items (or as they are from a source) without skipping any entry. Hence, we also model another abstract class SequencialIterator that inherits from SubjectIterator.

public abstract class SubjectIterator<T>
	where T : Subject
{
   public abstract IEnumerable<T> Next();
}

public abstract class SequencialIterator<T> : SubjectIterator<T>
   where T : Subject
{
   public int _min;
   public int _max;

   public SequencialIterator(int min = 0, int max = 1000)
   {
      _min = min;
      _max = max;
   }

   public override sealed IEnumerable<T> Next()
   {
      int index = _min;
      while (index <= this._max)
         yield return this.GetNext(index++);
   }

   protected abstract T GetNext(int index);
}

With the SequencialIterator we implement the Template Pattern. In this pattern we have a common algorithm or steps of an algorithm in the abstract class SequencialIterator. Those steps are usually implemented by the same abstract class or are abstract themselves. This provides an opportunity (a hook) for each of the subclasses to provide their own implementation and thus changing a step of the main algorithm. In our case the abstract step/hook is the GetNext(int index) function.

The SequencialIterator does not care how each subclass will get the next i-th entry. This responsibility is for each of the Iterators below:

public class SequencialNumbersIterator : SequencialIterator<Number>
{
   public SequencialNumbersIterator(int min = 1, int max = 1000) : base(min, max)
   {
   }

   protected override Number GetNext(int index)
   {
      return new Number(index++);
   }
}

public class SequencialBGGEntriesIterator : SequencialIterator<BGGEntry>
{
   public SequencialBGGEntriesIterator(int min = 0, int max = 100) : base(min, max)
   {
   }

   protected override BGGEntry GetNext(int index)
   {
      string path = Path.Combine(Path.GetDirectoryName(this.GetType().Assembly.Location), "../../../Resources/bgg_top_100.csv");
      var line = File.ReadLines(path).ElementAt(index + 1).Split(';').ToList();
      return new BGGEntry(line[2], Convert.ToDecimal(line[3]), Convert.ToInt32(line[5]));
   }
}

public class SequencialSongEntriesIterator : SequencialIterator<SongEntry>
{
   private readonly string _file;

   public SequencialSongEntriesIterator(string file, int max) : base(1, max)
   {
      this._file = file;
   }

   protected override SongEntry GetNext(int index)
   {
      string path = Path.Combine(Path.GetDirectoryName(this.GetType().Assembly.Location), "../../../Resources", _file);
      var line = File.ReadLines(path).ElementAt(index).Split(';').ToList();
      return new SongEntry(line[0], line[1], Convert.ToInt32(line[3]));
   }
}

For SequencialBGGEntriesIterator and SequencialSongEntriesIterator we use csv files that contains the information we want.

Because the SequencialIterator returns an IEnumerable<T> it can be used in a foreach statement.

The SubjectVisitor

The SubjectVisitor is responsible for translating each Subject to another form. In case of the original problem we will use ToTextRepresentation visitor in order to translate each number to the corresponding word. The SubjectVisitor has abstract methods for each type of Subject as shown below

public abstract class SubjectVisitor
{
   public abstract object VisitNumber(Number number);

   public abstract object VisitBGGEntry(BGGEntry bGGEntry);

   public abstract object VisitSongEntry(SongEntry songEntry);
}

Next, we define 3 visitors that will cover all the cases.

public class Rank : SubjectVisitor
{
   public override object VisitBGGEntry(BGGEntry bGGEntry)
   {
      return bGGEntry.Rating;
   }

   public override object VisitNumber(Number number)
   {
      return number.Value;
   }

   public override object VisitSongEntry(SongEntry songEntry)
   {
      return songEntry.Year;
   }
}

public class ToStringRepresentation : SubjectVisitor
{
   public override object VisitBGGEntry(BGGEntry bGGEntry)
   {
      return bGGEntry.Title;
   }

   public override object VisitNumber(Number number)
   {
      return number.Value.ToString();
   }

   public override object VisitSongEntry(SongEntry songEntry)
   {
      return songEntry.Title;
   }
}

public class ToTextRepresentation : SubjectVisitor
{
   // ... code omitted
   public override object VisitBGGEntry(BGGEntry bGGEntry)
   {
      return bGGEntry.Title;
   }

   public override object VisitNumber(Number number)
   {
      return this.NumberToWord(number.Value);
   }

   public override object VisitSongEntry(SongEntry songEntry)
   {
      return songEntry.Title;
   }

   // ... code omitted
}

From the above implementations we can see that in order to convert a number to word we use the ToTextRepresentation visitor and in order to convert a BGGEntry to Rating we use the Rank visitor.

The Operation

Finally, we would like a Strategy Pattern that will encapsulate the Summation and Average algorithms behind the IOperation interface.

The Solution

The Solution consists of all the previous components we mention. Below we present the final class diagram.

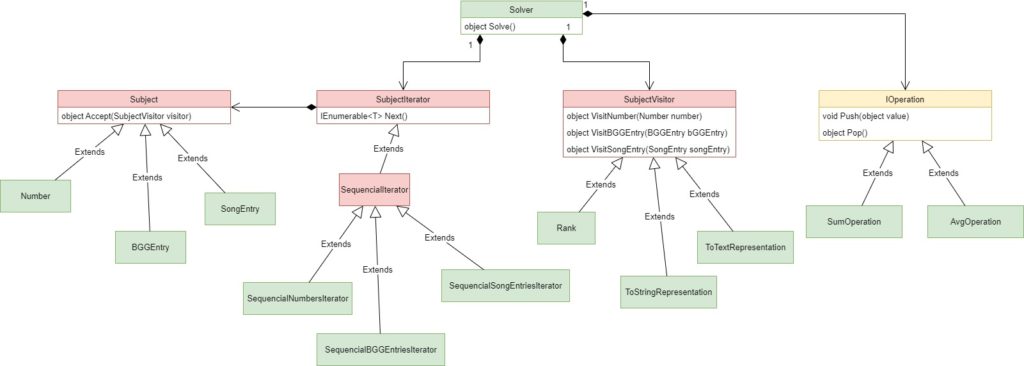
The real power comes from combining different building blocks in order to solve any case that belongs in the same group

Solving each case

Finally, in order to solve each case, we instantiate the Solver class with the appropriate services as shown below

Original Problem from Project Euler

ISolver solver = this.CreateSolverForProjectEuler();
var res = solver.Solve();

Solver<Number> CreateSolverForProjectEuler()
{
   return new Solver<Number>(
      new SequencialNumbersIterator(1, 1000), 
      new ToTextRepresentation(),
      new SumOperation());
}

answer:21124

Calculate the average of the first 100 numbers

var solver = this.CreateForAverageFirst100Numbers();
var res = solver.Solve();

Solver<Number> CreateForAverageFirst100Numbers()
{
   return new Solver<Number>(
      new SequencialNumbersIterator(1, 100),
      new Rank(),
      new AvgOperation());
}

answer:50.5

Calculate the average Rating of the first 100 BGG Entries

var solver = this.CreateForAverageFirst100BGGEntries();
var res = solver.Solve();

Solver<BGGEntry> CreateForAverageFirst100BGGEntries()
{
   return new Solver<BGGEntry>(
      new SequencialBGGEntriesIterator(0, 99),
      new Rank(),
      new AvgOperation());
}

answer:7.79

Calculate the average Title length of the first 100 BGG Entries

var solver = this.CreateForAverageTitleLenghtOfBGGEntries();
var res = solver.Solve();

Solver<BGGEntry> CreateForAverageTitleLenghtOfBGGEntries()
{
   return new Solver<BGGEntry>(
      new SequencialBGGEntriesIterator(0, 99),
      new ToStringRepresentation(),
      new AvgOperation());
}

answer:90.64

Calculate the total Title length of all Tool songs

var solver = this.CreateForTotalTitleLenghtOfToolSongs();
var res = solver.Solve();

Solver<SongEntry> CreateForTotalTitleLenghtOfToolSongs()
{
   return new Solver<SongEntry>(
      new SequencialSongEntriesIterator("tool_songs.txt", 70),
      new ToStringRepresentation(),
      new SumOperation());
}

answer:721